新説！ 地球から一番近い星は、金星ではなく水星である

・新しい点円法では、2つの惑星間の距離（時間平均）を正確に計算することができる。
・水星が、地球を含む太陽系の7つの惑星の中で、最も近い惑星であることがわかった。

皆さんは学校の授業で、地球に一番近い惑星は金星だと習ったのではないでしょうか。今ググってみても同じ答えが返ってくるでしょう。しかしながら、これは完全に正しいわけではないのです。金星は、時間的に平均すると最も近いわけではありません。

NASAの資料によると、金星は私たちに最も近い隣星であり、金星が地球に最も接近しているという意味ではその通りです。それでも、2つの惑星間の平均距離を考えると、もっと興味深いことがわかります。

最近、アラバマ大学とロスアラモス国立研究所の研究者たちは、2つの惑星間の距離（時間平均）を正確に決定する数学モデルを考案しました。このモデルにより、水星が地球に最も近い惑星であり、太陽系内の他の6つの惑星にも近いことがわかったのです。

数学的方法

従来の方法では、すべての惑星が同一平面上の軌道にあると仮定し、外側の軌道の平均半径から内側の軌道の平均半径を引くことで2つの惑星間の距離を計算します。これでは、最も近い点の平均的な距離しか得られません。

一方、新しい点円法では、2つの天体の軌道を共平面、円形、同心円と見なします。ある特定の時間における惑星の位置は、その軌道の確率的分布と考えることができます（図1a）。

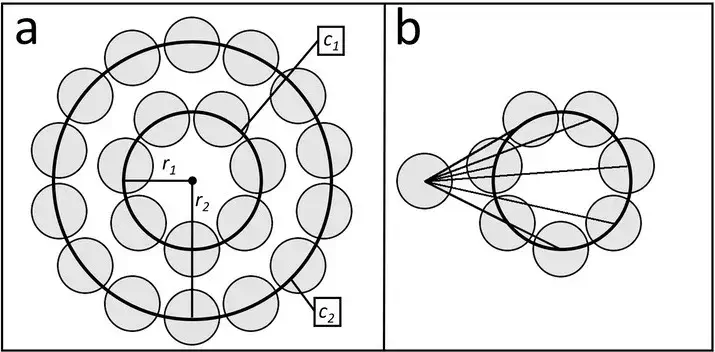
図1aと図1b

このように、2つの天体間の平均距離は、外側の円上の各点（c2）から内側の円上の各点（c1）までの平均距離を計算することで求めることができます。しかし、惑星の構造は回転対称であるため、外側の円上のどの点から内側の円上のどの点までの平均距離も同じになります（図1b）。

この方法では、任意の2つの軌道を持つ天体間の距離（時間平均）は、内側の軌道の相対半径に比例することがわかります。金星は太陽の周りをより近く（平均して）回っているため、水星よりも地球から遠くなります。

この方法を太陽系内のすべての惑星に適用したところ、水星が他の7つの惑星すべてに最も近い惑星であることがわかりました。水星と地球の平均距離は1.038 AU【天文単位】、金星と地球の平均距離は1.136 AUです。

検証結果

異なる方法による惑星間の平均距離（天文単位）の比較
出典：研究者

この結果を確認するため、研究者は8つの惑星の位置を1万年間マッピングするコンピュータでシミュレーションを行ったところ、1日後に、太陽系内のすべての惑星間の距離が記録されました。

このモデルは、同心円軌道、円軌道、同一平面上の軌道を持つあらゆる2つの天体に適用することができます。信号強度が距離の二乗に伴って著しく減少する衛星通信の中継を高速に計算するのに利用することが可能です。