毎年目にする、様々な新製品のほとんどは、古いテクノロジー【社会が持つ、物質文明に関する実用的な知識の総体】を使って開発されています。影響力のある科学者や数学者たちは、世界に一石を投じるために生まれました。
そして、彼らは自分たちの理論でそれを成功させ、それが現代テクノロジーの基礎を築いたのです。
この数十年で世界は大きく変わりましたが、それを可能にしたものは古い理論や発明に基づいています。この記事では、世界を変える上で重要な役割を果たしたテクノロジーの法則を、その影響と応用とともにご紹介します。
9. ピタゴラスの定理

歴史:ピタゴラスの定理は、ギリシャの数学者ピタゴラスによって初めて定式化され、解かれました。この定理は現在、何百もの証明があります。しかし、ピタゴラスの定理が一度に発見されたのか、異なる場所で異なる科学者によって複数回発見されたのか、その証拠はありません。
意味:直角三角形の斜辺の2乗は、他の2辺の2乗の和に等しい、とするものです。
応用:ピタゴラスの定理は三角法【三角形の角の大きさと辺の長さの間の関係の研究を基礎として、他の幾何学的図形の各要素の量的関係や、測量などへの応用を研究する数学の学問領域のひとつ】の基本です。また、GPSナビゲーション・システムにおいては、正確な測量と地図の作成に主に応用されています。
8. 微分積分学の基本定理
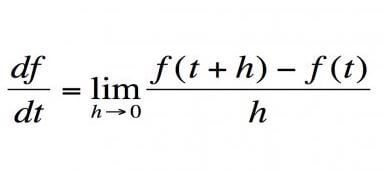
歴史:微分積分学の基本定理は微分と積分に基づいています。基本定理の最初の証明はジェームズ・グレゴリーとアイザック・バリーによって発表されました。現在の微積分のバージョンは、アイザック・ニュートン卿【イギリスの自然哲学、数学者、物理学者、天文学者、神学者】とゴットフリート・ライプニッツ【ドイツの哲学者、数学者】によって創始されました。
意味:微分と積分の概念を結びつける定理です。また、瞬間的な変化率を持つあらゆる計算を可能にします。
応用:この定理は医学、経済学、コンピュータ・サイエンスの分野で広く実用されています。最適解が要求されるあらゆる方程式で使われます。
7. ロジスティック・モデル

歴史:ロジスティック関数の曲線は、1844年にピエール=フランソワ・フェルフルスト【ベルギーの数学者】によって発表されました。初期段階では、グラフはほぼ指数関数的であり、飽和後は成長が止まります。
意味:S字型曲線としても知られており、その値は正の無限大と負の無限大の間にあります。式中のeは自然対数を表します。
応用:生物学、生態学、人工ニューラルネットワーク、確率、統計学、生物数学など幅広い分野で応用されているほか、天気予報にも使われます。
6. シャノンの情報定理

歴史:シャノンの情報定理は1948年、ベル研究所の技術者クロード・シャノンによって発表され、長距離通信のあり方を一変させました。
意味:シャノンの情報定理は、ノイズの存在下で情報を伝達できる最大速度を推定するもので、信号処理操作を含む応用数学の一分野です。
応用:現在、この定理は非可逆・可逆データ圧縮、バイオインフォマティクス【生命科学と情報科学の融合分野のひとつ】、音楽編集、情報検索などで広く使われています。インターネット、CD、携帯電話、数々の宇宙探査ミッションの成功と発展に大きな影響を与えています。
5. マクスウェルの定理
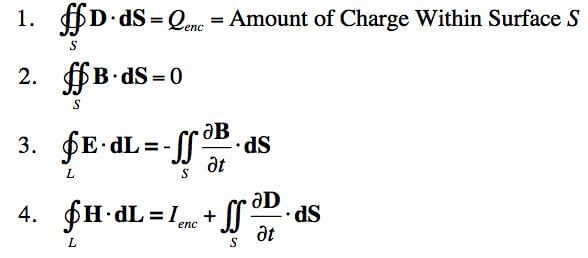
歴史:マイケル・ファラデー【イギリスの化学者、物理学者】、カール・F・ガウス【ドイツの数学者、天文学者、物理学者】、アンドレ=マリ・アンペール【フランスの物理学者、数学者】は、電気と磁気の関係について3つの異なる法則を示しました。ジェームズ・クラーク・マクスウェル【スコットランドの理論物理学者】が、これらの法則を式に変換し、相互に関連付けました。
意味:マクスウェルの4つの方程式はすべて、電界と磁界の関係を示しています。
応用:これらの方程式は、電磁波の性質やその他の技術の理解に大きな影響を与えています。現在でもテレビ、レーダー、現代の通信システムの製造に使われています。
4. フーリエ変換
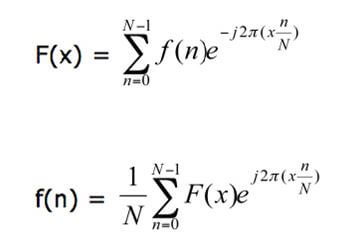
歴史:フーリエ変換は発見者ジョセフ・フーリエ【フランスの数学者、物理学者】にちなんで命名されました。彼は熱流と波動方程式からフーリエ変換の方程式を拡張しました。
意味:一般に、時間ベースの信号を周波数ベースの信号に変換するのに用いられます。この法則は、時間の信号パターンを周波数の関数として定義します。
応用:物理学、工学、量子力学、デジタル信号処理などに応用されています。
3. アインシュタインの相対性理論
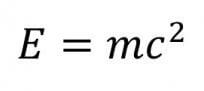
歴史:相対性理論はアルベルト・アインシュタイン【ドイツ出身の理論物理学者】によって発見されたもので、一般相対性理論と特殊相対性理論に分けられます。彼はヘンドリック・ローレンツ【オランダの物理学者】、アンリ・ポアンカレ【フランスの数学者、理論物理学者、科学哲学者】、アルバート・マイケルソン【アメリカの物理学者】によって得られた多くの理論的成果を利用しました。
意味:物体が放出するエネルギーは、物体の質量と光速の2乗の積に等しい、というものです。
応用:歴史上最も有名な方程式とされています。有名な例としては、全地球測位システム(GPS)が挙げられます。
2. 万有引力の法則

歴史:アイザック・ニュートンは、ヨハネス・ケプラー【ドイツの天文学者】からいくつかの資料を引用し、万有引力の法則を発見しました。ロバート・フック【イギリスの自然哲学者、建築家、博物学者、生物学者】の著作の盗用など、ニュートンの仕事に関する論争は多数あります。
意味:万有引力の法則によれば、宇宙における2つの物体の間に働く力は、それらの質量の積に正比例し、物体間の距離の2乗に反比例します。この法則は、宇宙のあらゆる2つの物体の間に働く力を計算するものです。
応用:この方程式は、重力に逆らうために使われます。宇宙ミッションでは、異なる物体が及ぼす力の最小値を求めるのに使われるほか、人工衛星の配置距離を求めるのにも用いられます。
1. ムーアの法則
歴史:この法則は、インテル社の共同設立者であるゴードン・E・ムーアにちなんで命名されました。彼は1965年に雑誌の記事で予言し、今では人々はそれを法則と考えています。
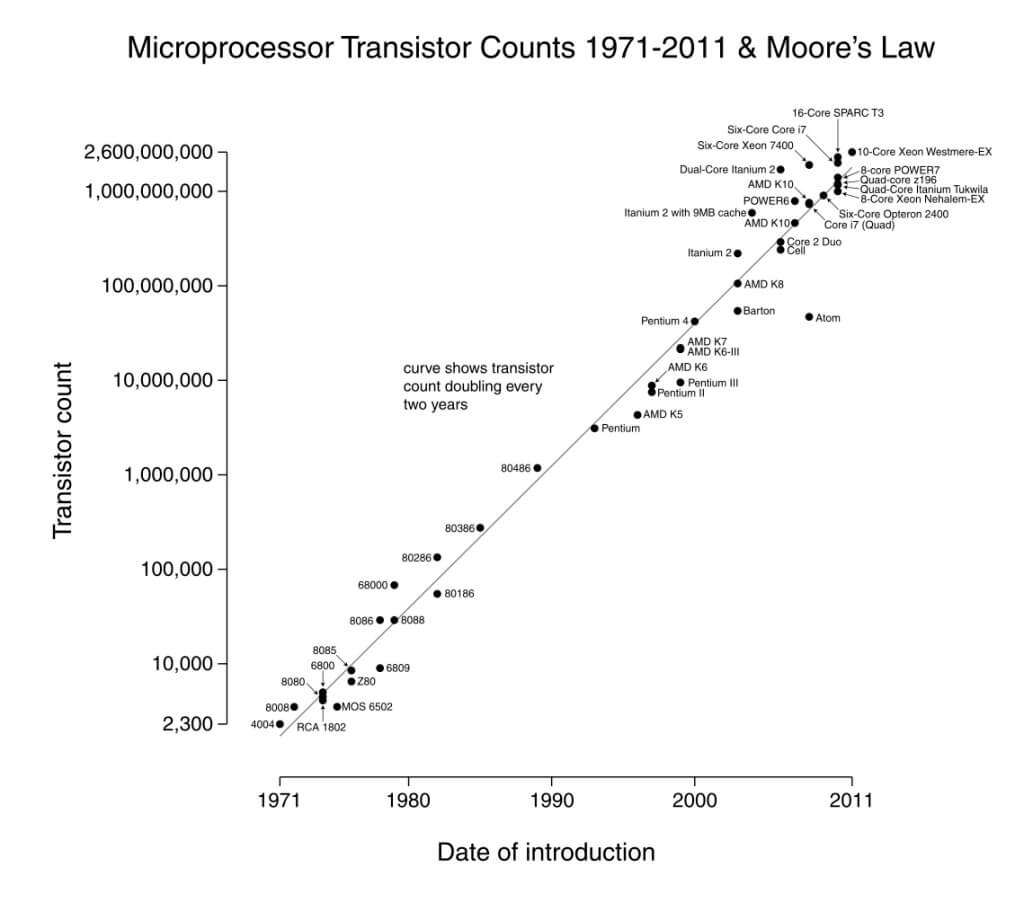
意味:ゴードン・E・ムーアは、集積回路基板のトランジスタ数は18ヶ月ごとに倍増すると予言しました。半世紀以上の後、2013年にこの法則は減速し、2020年以降はもう当てはまらないと予想されています。この法則には方程式はなく、通常は(1年とトランジスタ総数の間の)直線グラフで表されます。
応用:これは観察の法則であり、自然の法則ではありません。それでも、多くの企業が研究開発の目標を設定するのに役立ちました。どういうわけか、この法則は世界中の電子機器市場をも向上させたのです。